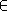
Exercice 1) On considère l'équation du premier ordre y' = y, avec et (t, y) × ₊ ^*.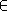

a) Rechercher toutes les solutions (I, f) (avec f de I dans ₊ ^*).

b) On se donne (t₀, y₀) 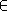× ₊ ^*. Rechercher toutes les solutions (I, f) satisfaisant la condition de Cauchy : t₀ 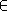I et f(t₀) = y₀.

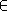
c) Reprendre les deux questions avec ₊ ^* et (t, y) × ₊.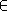

Exercice 2) On considère l'équation zz' = t, avec la donnée de Cauchy (t₀, z₀) = (0, 0). Déterminer les solutions maximales sur × ₊, et sur × .

Exercice 3) On considère l'équation (x + y) + (x - y)y' = 0 sur ².

a) Trouver les fonctions C¹ de ² dans dont la différentielle df en (x, y) soit (x + y)dx + (x - y)dy.

b) Soit (x₀, y₀) 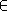² avec x₀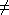y₀. Résoudre le problème de Cauchy associé.

c) Que peut-on dire si x₀ = y₀ ?

Exercice 4) Étudier puis résoudre les problèmes de Cauchy suivant :

a) tu' + u² = 1, u(4/) = -1 ;

b) u' = (t³ - t)e^-u, u(0) = 0 ;

c) 4tu'² = u² - 1, u(0) = 1;

d) u' = sin(u), u(0) = u₀ (en particulier étudier le cas y₀ ) ;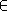

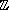Exercice 5) On considère l'équation a²y'² - t(1 + y'²) = 0 où a ₊ ^*.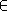

a) Réduire l'étude à a = 1.

b) Déterminer les solutions, par exemple à l'aide d'un paramétrag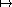e s(p(s), q(s)) de l'ensemble des couples (p, q) tels que q² - p(1 + q²) = 0. (Dessiner plusieurs courbes intégrales)

c) Que peut-on dire du problème de Cauchy ?

Exercice 6) On considère l'équation y² + (yy')² = a² où a ₊ ^*.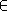

a) Montrer qu'une solution garde un signe constant. Réduire l'étude à a = 1 et U = × ₊ ^*.

b) Déterminer les solutions, par exemple à l'aide d'un paramétrag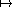e s(p(s), q(s)) de l'ensemble des couples (p, q) tels que p² + p²q² = 1. (Dessiner plusieurs courbes intégrales)

c) Que peut-on dire du problème de Cauchy ?

Exercice 7) On considère l'équation (v + xv')² - 4x²v' = 0

a) Étudier ses solutions, par exemple à l'aide d'un paramétrage s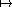(p(s), q(s)) de l'ensemble des couples (p, q) tels que (p + q)² - 4q = 0.

b) Discuter du problème de Cauchy de donnée (x₀, v₀) : nombre de solutions locales, nombre de solutions maximales.

Exercice 8) Déterminer les solutions de l'équation x²(xy' - y) = y² - x² par passage en coordonnées polaire (x, y) = (r cos(t), r sin(t)).

Exercice 9) On considère l'équation ff'' - 2f'² - f² = 0.

a) Chercher les solutions qui ne s'annulent pas à l'aide du changement de fonction g = f'/f. Discuter du problème de Cauchy.

b) Retrouver ces résultats à l'aide du changement de fonction h = f' f^-1. (f^-1 désigne ici la fonction réciproque de f, dans la mesure où cela a un sens)