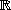 dans
dans 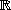 . On considère l'équation différentielle
:
. On considère l'équation différentielle
:
Exercice 1) Soit f et g deux fonctions de classe C1 de 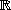 dans
dans 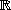 . On considère l'équation différentielle
:
. On considère l'équation différentielle
:
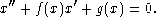
a) Écrire cet équation sous la forme d'un système du premier ordre pour (x, y) = (x, x').
On fait les hypothèses de frottement et de rappel
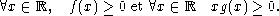
b) Déterminer G pour que E(x, y) = y2/2 + G(x) soit une intégrale première quand f est la fonction nulle.
c) Montrer que sous l'hypothèse de frottement, E décroit le long des trajectoires, et que sous l'hypothèse de rappel, 0 est un minimum de E.
d) Montrer que si f(0) > 0 et xg(x) = 0 sur un voisinage K de 0 dans 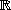 , alors 0 est un point
d'équilibre stable.
, alors 0 est un point
d'équilibre stable.
e) Montrer que si f(x) > 0 et xg(x) > 0 sur un voisinage K de 0 dans 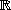 , alors E est une fonction
de Liapounov et 0 est asymptotiquement stable. Peut-on encore affaiblir l'hypothèse sur g
?
, alors E est une fonction
de Liapounov et 0 est asymptotiquement stable. Peut-on encore affaiblir l'hypothèse sur g
?
f) Donner une condition suffisante pour que toute solution converge vers 0 quand t 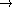
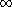 .
.
g) Application aux systèmes
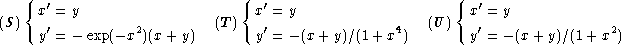 |
Exercice 2) Étude qualitative des systèmes
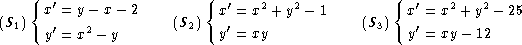 |
 -
- )
)