
Project maintained by François Jauberteau, Yann Rollin and Samuel Tapie
This is the homepage of the software Discrete Moment Map Flow, announced in our research paper
Discrete Geometry and Isotropic Surfaces.
Our research led us to consider an evolution equation for surfaces in the four dimensional Euclidean space. The expected generic behavior of the corresponding flow is to converge towards Lagrangian surfaces in $ \mathbb{R}^4$. Instead of tackling this open problem from the point of view of PDE and global analysis, we considered an analogous finite dimensional problem in the context of discrete symplectic geometry. This field is still at its early stages and many geometers are interested in developping the discrete counterpart of symplectic geometry.
Our program is based on the Euler method applied to a discrete version of the flow. Discrete surfaces of $\mathbb{R}^4$ are represented by quadrangular meshes. These meshes evolve under an ordinary differential equation introduced below. For more informations, you are encouraged to read our research paper. However we provide a short reminder of the objects, for the user's convenience. If you would like to skip the mathematical introduction, you may proceed directly to the download section.
When running the program, the user observes the discrete flow evolving in realtime. The user can interact with various parameters (time step, scaling, number of faces, etc...) using the mouse and keyboard. The initial data of the flow is chosen from a library of parametrized tori in the $ 4$-space. These examples can be modified randomly with a variable amount of noise. Little programming background is needed to add other types of tori to the native library.
In all experiments that we have made, we observe a converging flow, were the limit is a Lagrangian quadrangular mesh, unless the time parameter is too big. In such case, the flow may blow-up in finite time. This behavior can always be avoided (experimentaly) by decreasing the time step.
In conclusion, the DMMF program produces large classes of discrete Langrangian surfaces, or strictly speaking, Lagrangian quadrangular meshes, which were not known before and provide fundamental examples for symplectic geometers and topologists.
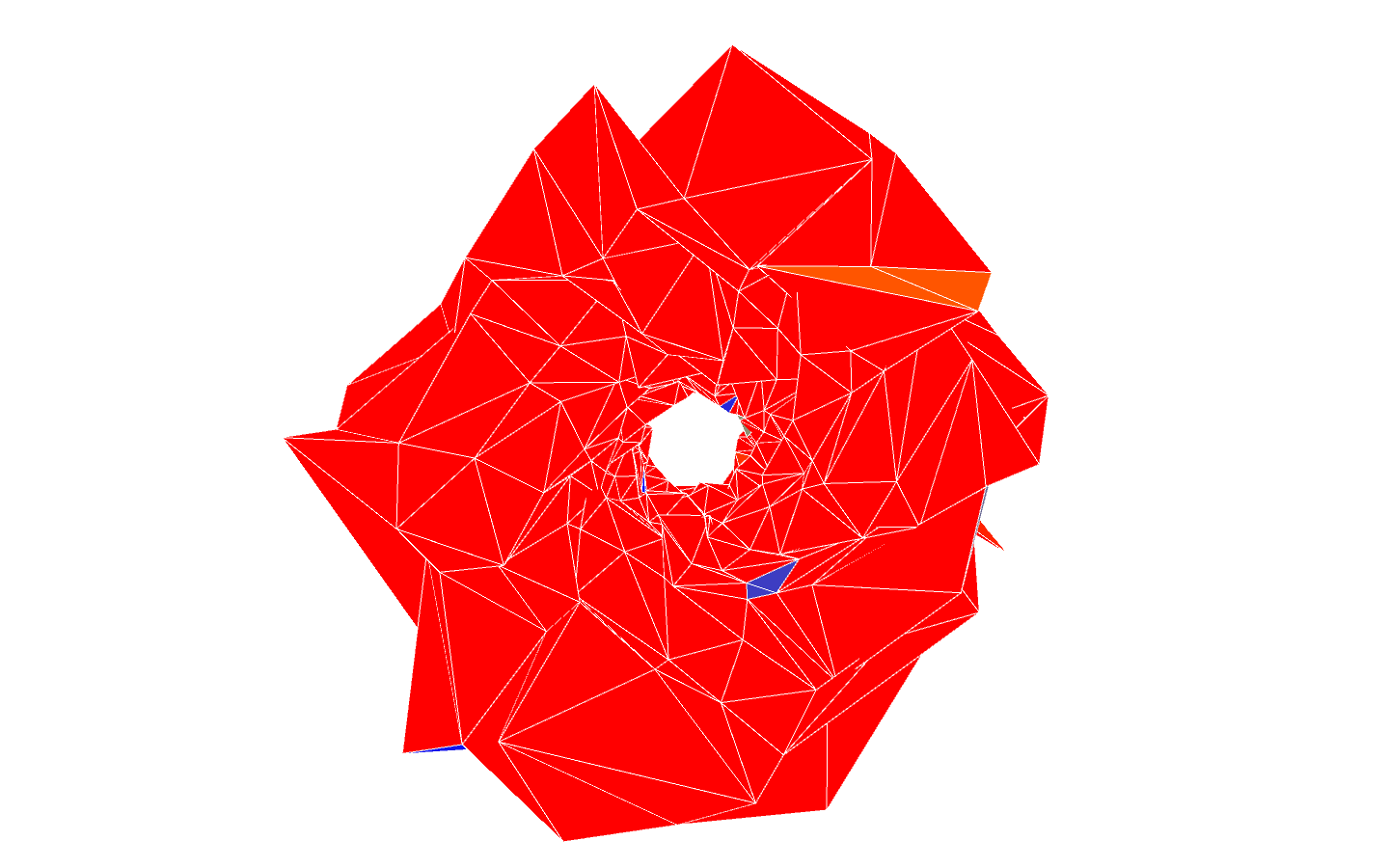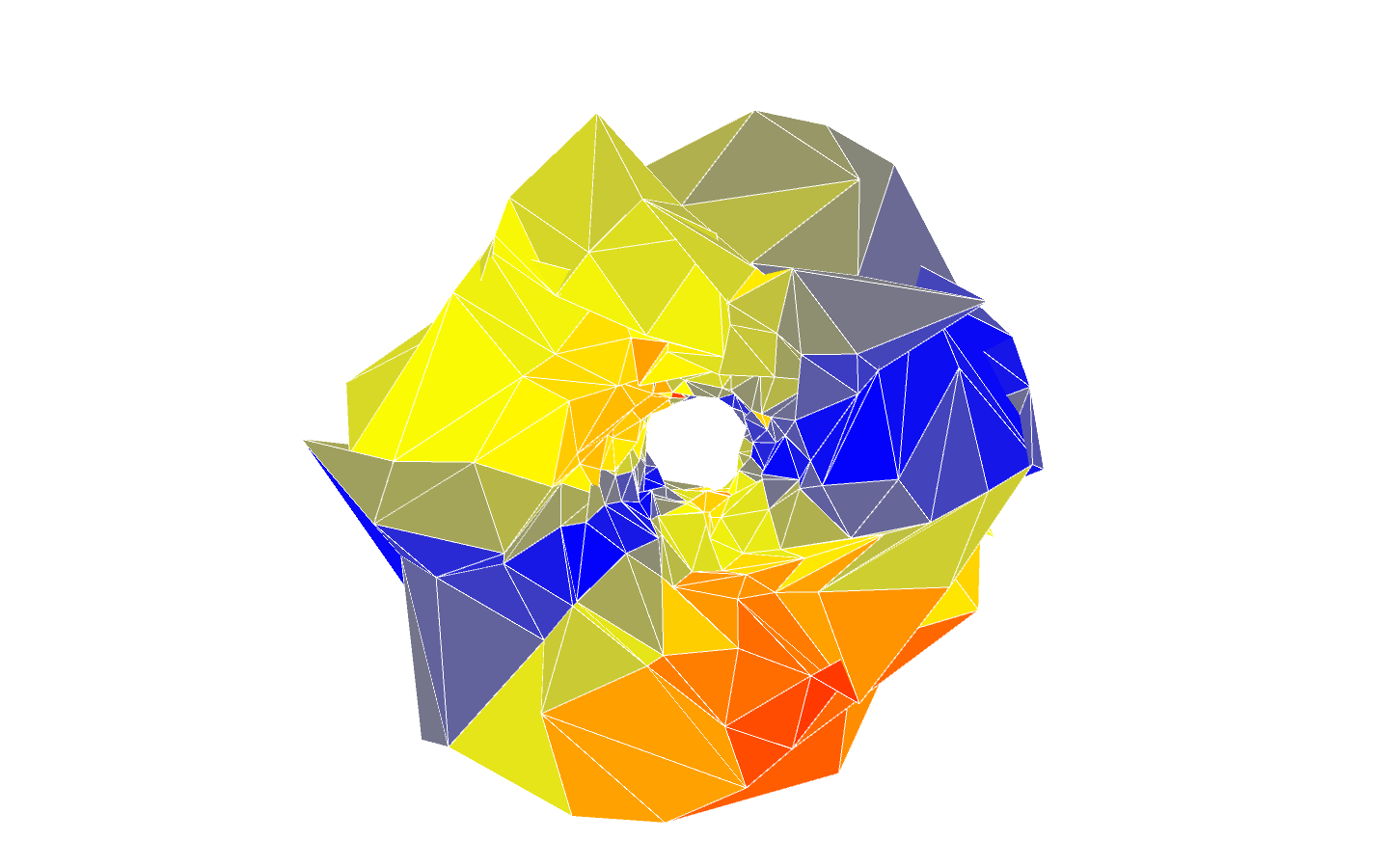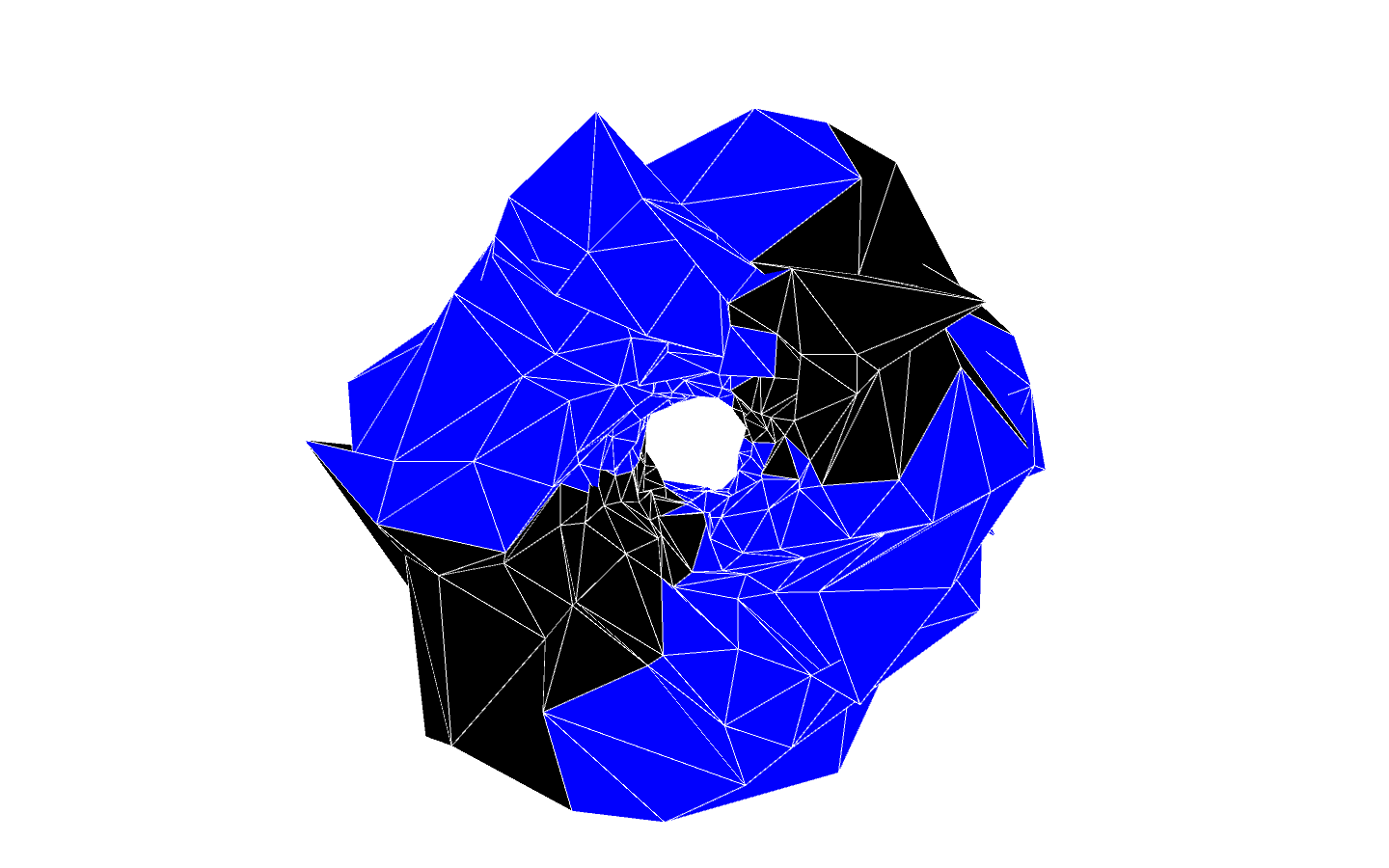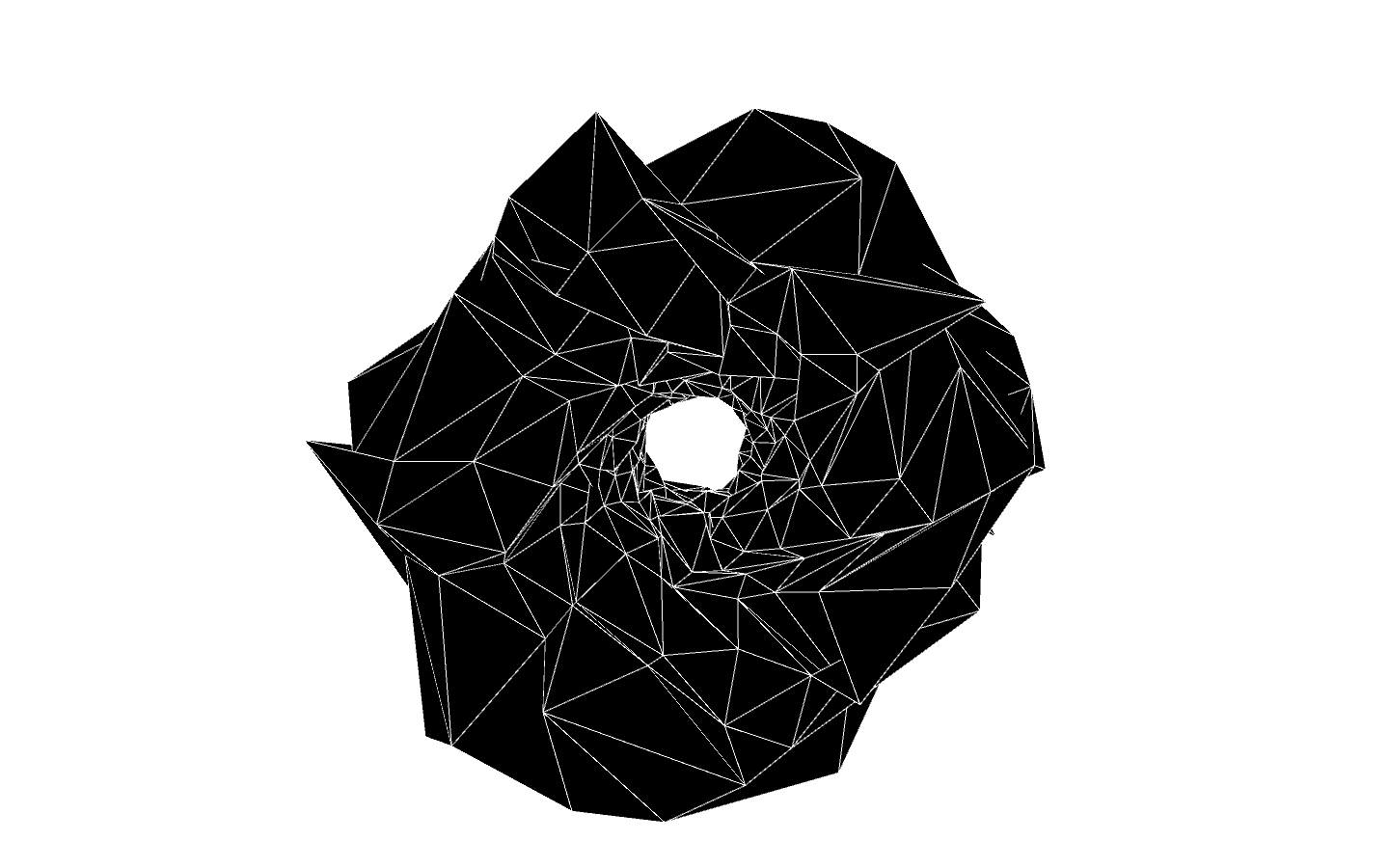
The animated picture below shows a few screenshots of the flow, starting from noisy Clifford torus. The faces are colored according to the symplectic density. If the density is greater than 1, the color is red. As the density decreases, the color becomes yellow then blue. If the density is smaller that $ 10^ {-3}$, the color suddenly becomes black, to show that we have obtained a surface which is very close to be Lagrangian.
The picture below shows a quadrangular mesh, which is very close to be Lagrangian. The torus has size of order 1 whereas its sympectic density is of order $ 10^{-8} $. The original parametrization is obtained by considering the boundary of a tubular neighborhood of the trefoil knot in $ S^3 $. The discrete moment map flow produced this Lagrangian mesh as the limit.

The picture below shows another Lagrangian quadrangular mesh where, instead of a trefoil knot, we consider a (3,5)-torus knot. Again, this example has size of order 1 and a sympectic density is of order $ 10^{-8} $.

Surfaces of $\mathbb{R}^4$ are implemented as some kind of quadrangular meshes. More precisely, we consider the standard lattice $$\Lambda_N =\mathbb{Z} \cdot \frac {e_1}N \oplus \mathbb{Z} \cdot \frac {e_2}N, $$ defined for positive integers $ N $, where $(e_1,e_2)$ is the canonical basis of $\mathbb{R}^2$. The lattice $\Lambda_N$ is regarded as the set of vertices of the standard quadrangulation $\mathcal{Q}_N(\mathbb{R}^2)$, which is the usual quadrangulation of $\mathbb{R}^2$ tiled by squares of size $ N ^{-1}$. The lattice $\Lambda_N$ descends a discrete subgroup of the torus $$\Sigma =\mathbb{R}^2/\Lambda_1$$ and the quadrangulations $\mathcal{Q}_N(\mathbb{R}^2)$ also descend to the quotient as quadrangulations $\mathcal{Q}_N(\mathbb{\Sigma})$ of $\Sigma$. The real vector spaces of cocyles on the quadrangulations are denoted $ C^i(\mathcal{Q}_N(\Sigma))$, where $ i=0,1,2 $ for vertices, edges and faces. The space of quadrangular meshes is defined as $$ \mathscr{M}_N = C^0(\mathcal{Q}_N(\Sigma))\otimes \mathbb{R}^4. $$ A mesh $\tau\in \mathscr{M}_N$ is an object that associates $\mathbb{R}^4$-coordinates to each vertex of the quadrangulation.
The space $ C^0(\mathcal{Q}_N(\Sigma))$ is endowed with an inner product $ \langle \! \langle \cdot,\cdot \rangle\! \rangle $, with the convention that the dual of basis of the vertices of $ \mathcal{Q}_N(\Sigma)$ is orthogonal and each dual vertex has norm square $ N^{-2} $. The space $ C^2(\mathcal{Q}_N(\Sigma)$ is endowed with a similar inner product denoted $ \langle \! \langle \cdot,\cdot \rangle\! \rangle $ as well. Together with the standard Euclidean metric $ g$ and complex structure $ J$ of $\mathbb{R}^4\simeq \mathbb {C}^2$, this provides a canonical inner product on $\mathscr{M}_N$ and a complex structure, denoted $ J $ in the same way. We consider the quadratic map $$ \mu_ N ^ r : \mathscr{M}_N \longrightarrow C^2(\mathcal{Q}_N(\Sigma)), $$ which associates to each face of a quadrangular mesh $ \tau $ its symplectic given by $$ \langle \mu_ N ^r ( \tau ) , f \rangle = N^2 S ( f, \tau ), $$ where $ S $ is the symplectic area of a quadrialteral, defined as the integral of the Liouville form along the quadrilateral of $ \mathbb{R}^4 $. Alternatively $ S$ is also the symplectic area of any compact surface of $ \mathbb{R}^ 4$ with boundary given by the quadrilateral. We are interested in Lagrangian quadrangular meshes, defined as the solutions of the equation $$ \mu_N^r(\tau)=0. $$ Lagrangian quadrangular meshes of $\mathbb{R}^4$ are discrete analogues of smooth immersed Lagrangian tori of $\mathbb{R}^4$. The program DMMF, based on an evolution equation for quadrangular meshes, produces, in the limit, Lagrangian quadrangular meshes.
The finite difference operator $$ \delta_\tau : T_\tau\mathscr{M}_N\longrightarrow C^2(\mathcal{Q}_N(\Sigma)), $$ given by $$ \delta_\tau = -D\mu_N^r|_\tau \circ J $$ is explicitely computed as $$ \delta_\tau V = \frac{N^ 2}2 \sum_{v,f} g \left (V(v), D^ {\tau}_{v,f} \right )f^*. \tag{*}\label{eq:delta} $$
The space of meshes is endowed with a flow, which is given by the ordinary differential equation with smooth coefficients: $$ \frac{d\tau }{dt} = J \delta^ \star_\tau \mu_N^r(\tau). \tag{F}\label{eq:flow} $$ This flow is a finite dimensional version of a flow related to the moment map geometry of an infinite dimensional space, introduced by Simon Donaldson (cf. our article, Section 2, for more details about this fact). The above equation $ \eqref{eq:flow}$ is just a downward gradient flow which may be expressed as $$ \frac{d\tau }{dt} = -\frac 12 J \mathrm{grad}\| \mu_N^r \|^2, $$ where the norm and gradient are defined using the canonical inner products. The fixed points of the flow correspond to quadrangular meshes solution of the problem $$ \delta^\star_\tau \mu_N^r(\tau) = 0. \tag{***} \label{eq:fp} $$ From an experimental perspective, it seems that $\ker\delta^\star_\tau$ reduces to constant functions. We point out that this fact is known to be true if the quadrangular mesh $ \tau$ is sufficiently close, in some sense, to a smooth nondegenerate immersion (cf. our research paper for more details). This is also true under some mild genericity assumption of the mesh $ \tau$. It follows that Equation $ \eqref{eq:fp}$ forces $\mu_N^r(\tau)=cst$ which implies $\mu_N^r(\tau) =0$ by Stokes theorem. In other words, fixed points of the flow $ \eqref{eq:flow} $ appear to be, at least generically, Lagrangian quadrangular meshes.
We have not carried out any thorough study of the ODE $ \eqref{eq:flow}$, but we expect that its flow should converge generically. Instead we provide a numerical simulation of the flow which seems to confirm this behavior.
We provide a numerical simulation of the flow $ \eqref{eq:flow}$ by the most rudimentary technique at hand, the Euler method. We choose a small time interval $ \Delta t>0$. Given a quadrangular mesh $\tau_i $ at time $ t_i= i\Delta t$, we define the quadrangular mesh $\tau_{i+1}$ at time $ t_{i+1}=t_i + \Delta t$ by induction as $$ \tau_{i+1}=\tau_i + \Delta t \cdot J \delta_{\tau_i}^\star \mu_N^r(\tau_i). \tag{DF}\label{eq:dflow} $$ The discrete flow $ \eqref{eq:dflow}$ is obtained as a discretization of the flow $ \eqref{eq:flow}$ via an explicit finite difference method of order $ 1$. Consequently, as $\Delta t\rightarrow 0$, this technique provides an approximation of the flow lines of the ODE. This scheme is simple to code on a computer. The elements of the vector space $\mathbb{R}^4$ are coded as $ 4\times 1$ arrays with float (or double) entries called $ V4d$. We store $\tau_i$ as an $ N\times N$ array with entries of $ V4d$-type. Given $\tau_i$, the diagonals of each faces are readily computed from the knwoledge of the vertices of each quadrilateral of $\mathbb{R}^4$. These diagonals are used in turn to compute the value of $\mu_N^r(\tau_i)$ and apply the operator $\delta_{\tau_i}^\star$. From this stage, one can compute $\tau_{i+1}$ and iterate the discrete numerical flow.
The discrete flow $ \eqref{eq:dflow}$ can be implemented using most programming languages with sufficient floating point number accuracy. The algorithm is very fast with linear complexity in the data size $ N^ 2$. With a current personal computer, we may obtain smooth real time movies, with more than $ 24$ frame per second, of the evolving surface with $ N\leq 50$, that is for a surface with $2 \, 500$ quadrilaterals.
The last task is to produce a variety of initial data $\tau_0$ to start the discrete flow. The idea is to use a collection of smooth maps from the torus to $\mathbb{R}^4$. For example parametrizations of the Clifford torus, the Chekanov torus, the boundary of tubular neighborhood of $ (p,q)$-torus knots, and several other smooth maps more or less arbitrary. We consider the disrete samples of these smooth maps as initial value $\tau_0$. The corresponding parametrizations are explicitely given in the section below. It is also useful to apply some noise to $\tau_0$. Indeed, the Clifford and Chekanov tori are already Lagrangian. It follows that the corresponding sample mesh are almost Lagrangian and the flow seems to be still. A random pertubation shows what type of stability one can expect. A difficulty with the discrete flow is that it may blow up in finite time, in particular if the time step $\Delta t$ is big compared to the noise or to the symplectic density.
One of the less natural aspect of the program is to choose a representation of surfaces on a computer screen. For this purpose, we need to choose a projection on a $ 3$-dimensional submanifold of $\mathbb{R}^4$. Our choice, which may not be the best in certain situations, is the following: we consider the radial projection of $\mathbb{R}^4$ on the $ 3$-sphere $ S^3$ of radius $ 1$ centered at the origin. The sphere minus a point admits a stereographic projection onto $\mathbb {R}^3$, understood as a tangent space to the sphere. Composing the radial projection and the stereographic projection provides a quadrangular mesh with $\mathbb{R}^3$-coordinates. One can precompose the projection with rotations of $\mathbb{R}^4$ around two arbitrary planes of $\mathbb{R}^4$ connected to mouse motions -- we are limited here with the two dimensional motions of the mouse. This basic interactive mouse action allows the user to see the surface from different angles. Eventually, we rely on OpenGL to render a representation of the surface, in perspective, on a computer screen.
These operations are easily implemented. Given the quadrangular mesh $\tau_i$ we compute a projected quadrangular mesh $\tau'_i$ with $\mathbb{R}^3$-coordinates. Such coodinates are implemented with a type $ V3d$, given by $ 3\times 1$ array wit float (or double) entries. Then $\tau'_i$ deduced from $\tau_i$ as an $ N\times N$ array with $ V3d$-entries. A quadragular mesh of $\mathbb{R}^3$ is easily represented in perspective using the OpenGL library. We merely need to make a choice of how to represent quadrilaterals of $\mathbb{ R}^3$. Indeed, they are generally not flat. Our program spilts each quadrilateral along an arbitrary diagonal and draws the two distinct triangles for each quadrilateral. We choose a color gradient to fill each triangle which depends on the value of $\mu_N^r$. If the abolute value of the symplectic density of the face is sufficiently small, that is $ 10^{-3}$ in the case of our program, we choose a final color, for instance black, which shows that we reached our target. We insists that such triangles do not correspond in any ways to Lagrangian triangles of $ \mathbb{R}^4$. They merely permit to draw a surface in $ \mathbb{R}^3$ with a given $ 1$-skeleton.
The choice of language for implementing the above scheme had to be done carefully. We were looking for a versatile programming language, which should be:
An effortless language that meets these needs is the Java dialect Processing3. Our DMMF code for version 0.6 is about 1000 lines only, which we consider rather short. We became aware of this language and its capabilities in 2014, when attending a screening of C4I, at le musée d'art comtemporain de Montréal, a movie and musical piece by the artist Ryoji Ikeda.
The code is freely distributed under the terms of the GNU GPL licence. We do not provide any support or warranty. We recommend using directly the source code compiled with the Processing3 programming IDE. There are also compiled versions of the code below. However, they are not up to date and may not work on your platform.
Installation notes:
| Key | Function |
| Mouse | Rotate the surface in $ \mathbb{R}^ 4$ about 2 arbirarily chosen planes. |
| Spacebar | Run or stop the flow. |
| h | Toggle the help page for key functions |
| i | Toggle the information page. Many informations are printed on screen, including framerate, torus type, maximum symplectic density... |
| r | Restart the flow from time zero. |
| d/D | Decrease of increase the time step. |
| q/Q | Decrease or increase the number of quads of the mesh. |
| n/N | Decrease or increase the random noise level. |
| t/T | Change the initial surface type. |
| s/S | Decrease or increase the overall scaling factor. |
| f | Toggle the filling mode for faces of the mesh. |
| b | Toggle drawing balls at the vertices. |
| p | Save a screenshot in the scketch directory. |
| m | (pressed continuously) -- save a movie in the sketch directory. The sequence of .tiff screenshots can be converted to a .mov format using the IDE tool MovieMaker. |
| c/C | Decrease or increase the number of iterations of the flow computed between each frame. |