Examen de Janvier 2002-LMA-MM1

Exercice 1. Commenter chaque instruction et expliquer ce que font les subroutines dans le module suivant

  MODULE Janvier02
      IMPLICIT NONE
      TYPE Postale
         CHARACTER (LEN = 30) :: ville
         INTEGER              :: code
      END TYPE Postale
      
      CONTAINS
        RECURCIVE SUBROUTINE Mystere (Tab)
            TYPE(Postale), DIMENSION (:), INTENT(INOUT) :: Tab
            INTEGER                                     :: Taille
            INTEGER, DIMENSION(1)                       :: Grand
                    
            Taille= SIZE(Tab)
            IF (Taille > 0) THEN
               Grand = MAXLOC(Tab(:)%code)
               CALL Swap (Grand(1), Taille)
               CALL Mystere (Tab(1:taille-1))
            ENDIF            
            CONTAINS
                 SUBROUTINE Swap(I,J)
                    INTEGER, INTENT(IN) :: I,J
                    TYPE(Postale)       :: Tamp
                    Tamp = Tab(I)
                    Tab(I) = Tab(J) 
                    Tab(J) = Tamp
                 END SUBROUTINE Swap
        END SYBROUTINE Mystere
  END MODULE Janvier02

Si $Tab$ est de taille 4, donner un exemple d'initialisation du tableau. Ensuite, imprimer le tableau après l'appel de la subroutine Mystere(Tab).

Exercice 2.

1. Ecrire sous forme d'une boucle explicite l'instruction suivante :

      L(J:k+1, k-1:I+k) = V( J-2:k-1, 1:I+2)*W( I+J+5:I+k+6, J+1:J+I+2)
   

2. En utilisant les constructeurs des tableaux, initialiser un tableau de réels contenat les nombres 1 à 9.5 par pas de 0.5.
3. Soient I = 99, J = 121, x = 3.35 , y = 104.E-2 , en notant un espace par $\cup$, effectuer les print suivants

        write(*,'(I5,I5)')I,J
        write(*,'(I5,4/,I5)')I,J
        write(*,'(F8.2,2X,E12.4)')x,y
   

Exercice 3.

Soit $A$ une matrice creuse telle que $a_{i,j} = 0$ pour $j \ne i,i-1,i+1,i- 2$. On stocke alors la matrice sous la forme

        REAL, DIMENSION(N,4) :: A

et on désigne par

A(i,1)	la sous-sous-diagonale	($a_{i,i-2}$, i=3,n )
A(i,2)	la sous-diagonale	($a_{i,i-1}$, i=2,n )
A(i,3)	la diagonale	($a_{i,i}$, i=1,n)
A(i,4)	la sur-diagonale	($a_{i,i+1}$, i=1,n-1)

Dans la suite de l'exercice, toutes les matrices utilisées sont stockées sous cette forme.

1. Ecrire une fonction nommée FUNCTION TRACE(A) permettant de calculer la trace d'une matrice A. On rappelle que $trace(A) = \sum_{i = 1}^{N}a_{i,i}$

2. Ecrire une fonction FUNCTION NORME(A) permettant de calculer la norme infinie d'une matrice A. On rappelle que $$\Vert A\Vert _\infty = \max_{i=1,N} (\sum_{j =1}^N \vert a_{i,j}\vert )$$.

3. Ecrire une fonction ( nommée mv(A,x)) qui effectue le produit de la matrice A par un vecteur x ( notez que seul $A$ et $x$ sont transmis en arguments).

4. Ecrire une 'interface operator(*)' permettant de rendre l'opération $y=A*x$ valide.

5. Pour résoudre le système linéaire $Ax =b$ , on considère l'algorithme de Jacobi suivant
   $$\left\{ \begin{tabular}{l} $x_0$ arbitraire\\ $x_{k+1} = x_k -D^{-1}Ax_k+ D^{-1}b $ \end{tabular} \right .$$
   avec $D^{-1}$ la matrice formée de la diagonale de $A$. On considère comme test d'arrêt pour cette méthode itérative $\Vert x_{k+1} - x_{k}\Vert \leq \varepsilon.$

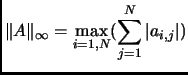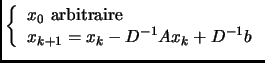
   Ecrire une fonction : FUNCTION Jacobi (b, A) permettant de calculer $x$. On pourra écrire dans un module une surdéfinition de l'opérateur ($/$), afin que l'opération suivante $x = b/A$ soit valide.

6. Proposer un programme permettant de lire $A$ et $b$, résoudre le système linéaire $Ax =b$ et d'imprimer le résultat dans un fichier de sortie.