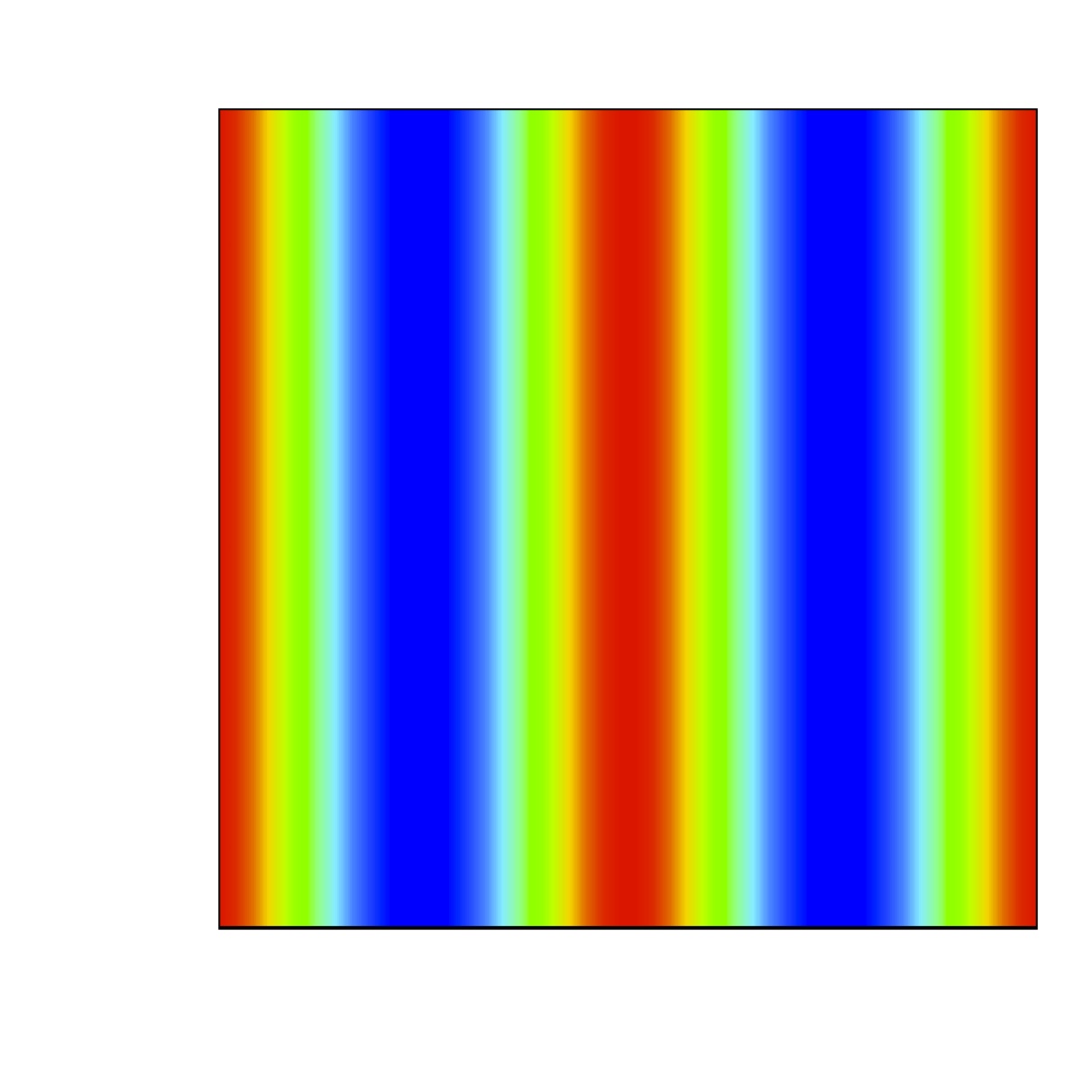
Mazen
Saad
in
collaboration with Mostafa Bendahmane
Our motivation is a mathematical
model describing the spatial propagation of an epidemic disease
through a population. In this model, the pathogen diversity
is structured into two clusters and then the population is divided
into eight classes which permits to distinguish between the
infected/uninfected population with respect to clusters. In this
paper, we prove the weak and the global existence results of
the solutions for the considered reaction-diffusion system
with Neumann boundary. Next, mathematical Turing formulation
and numerical simulations are introduced to show
the pattern formation for such systems. For more information see
here.
A system of reacting and diffusing
chemicals can interact and produce a stable nonuniform patterns in
space.
Diffusion is usually considered to be a stabilizing process, but
Turing's idea is, under certain conditions (Turing conditions),
spatially inhomogeneous patterns can evolve by diffusion driven
instability.
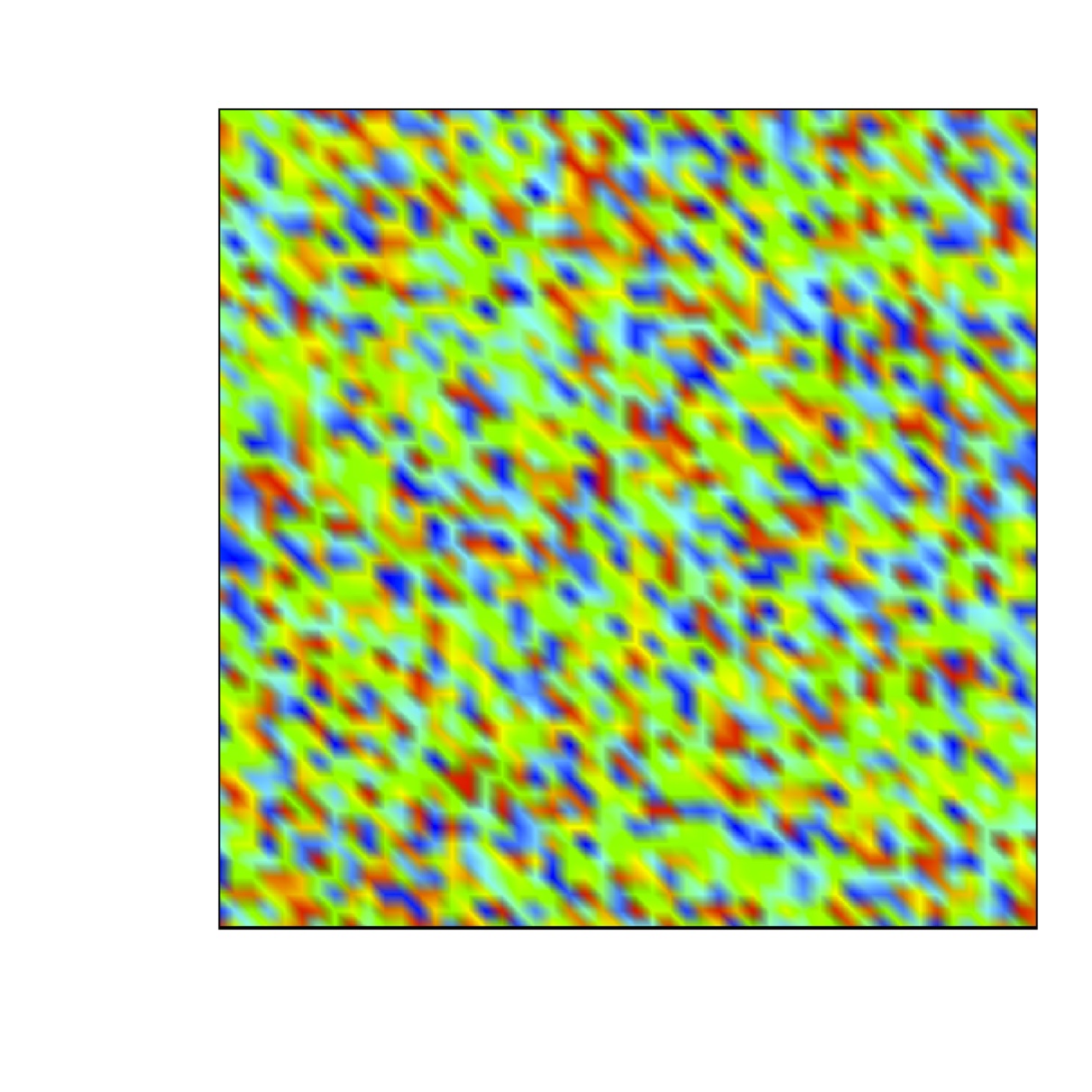
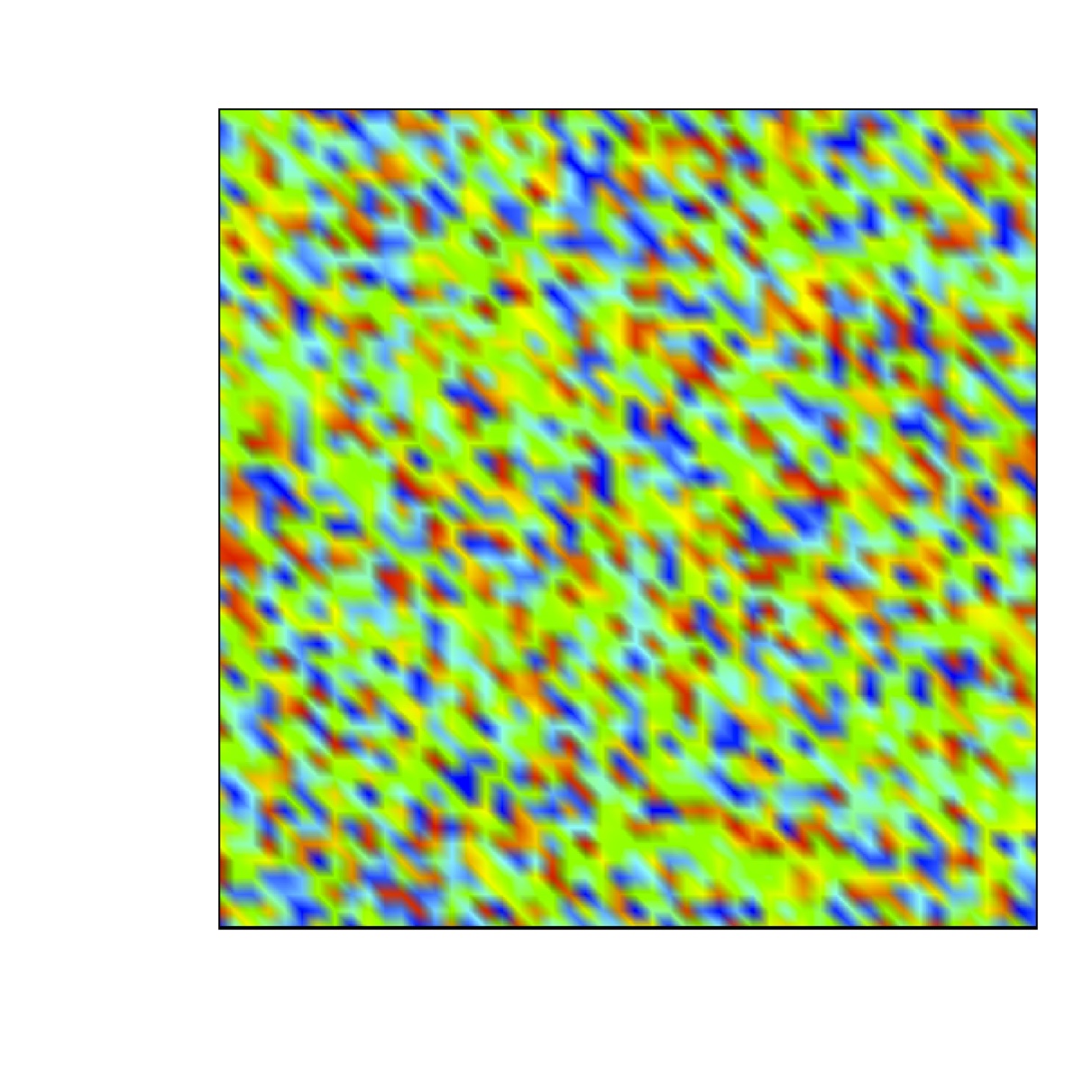
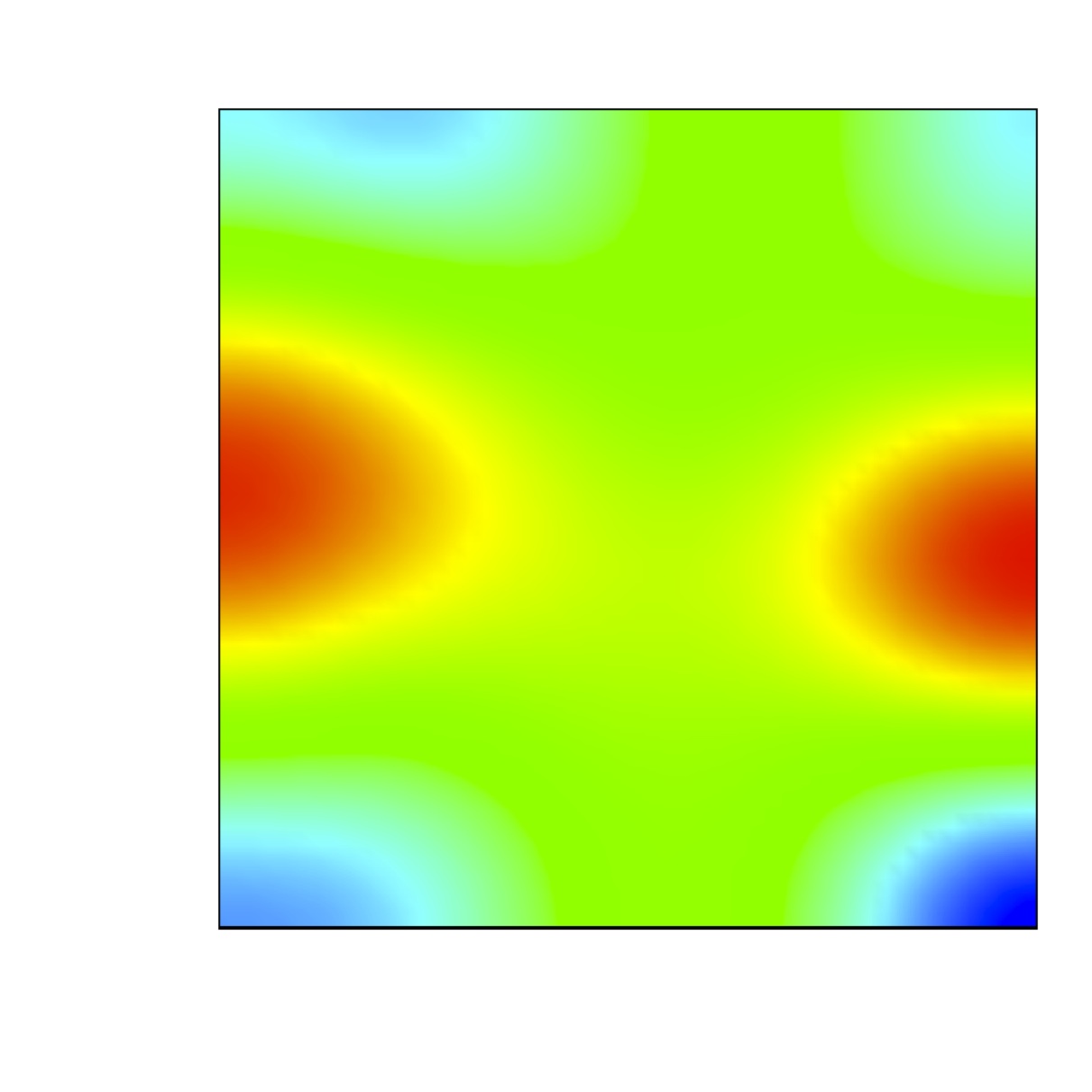
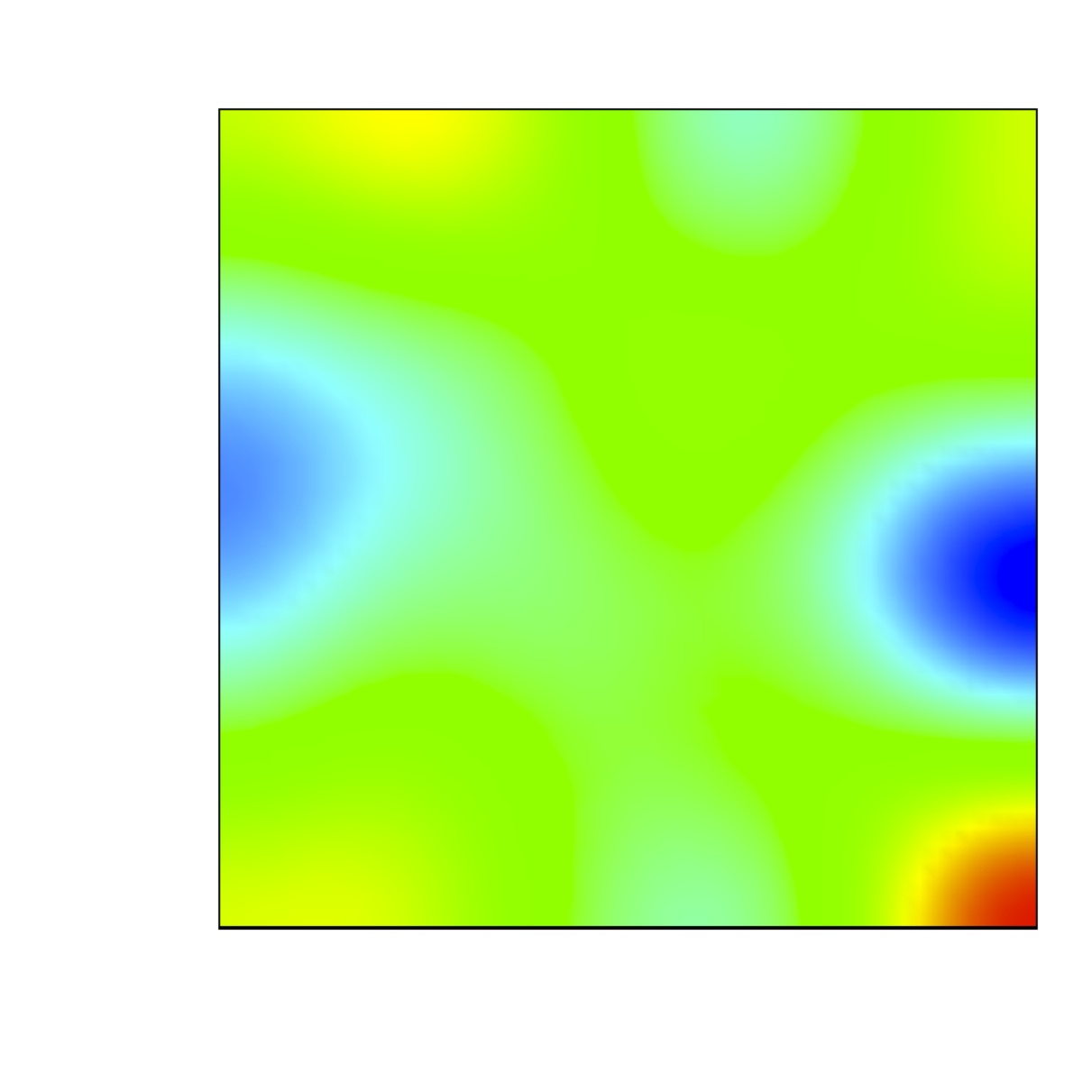
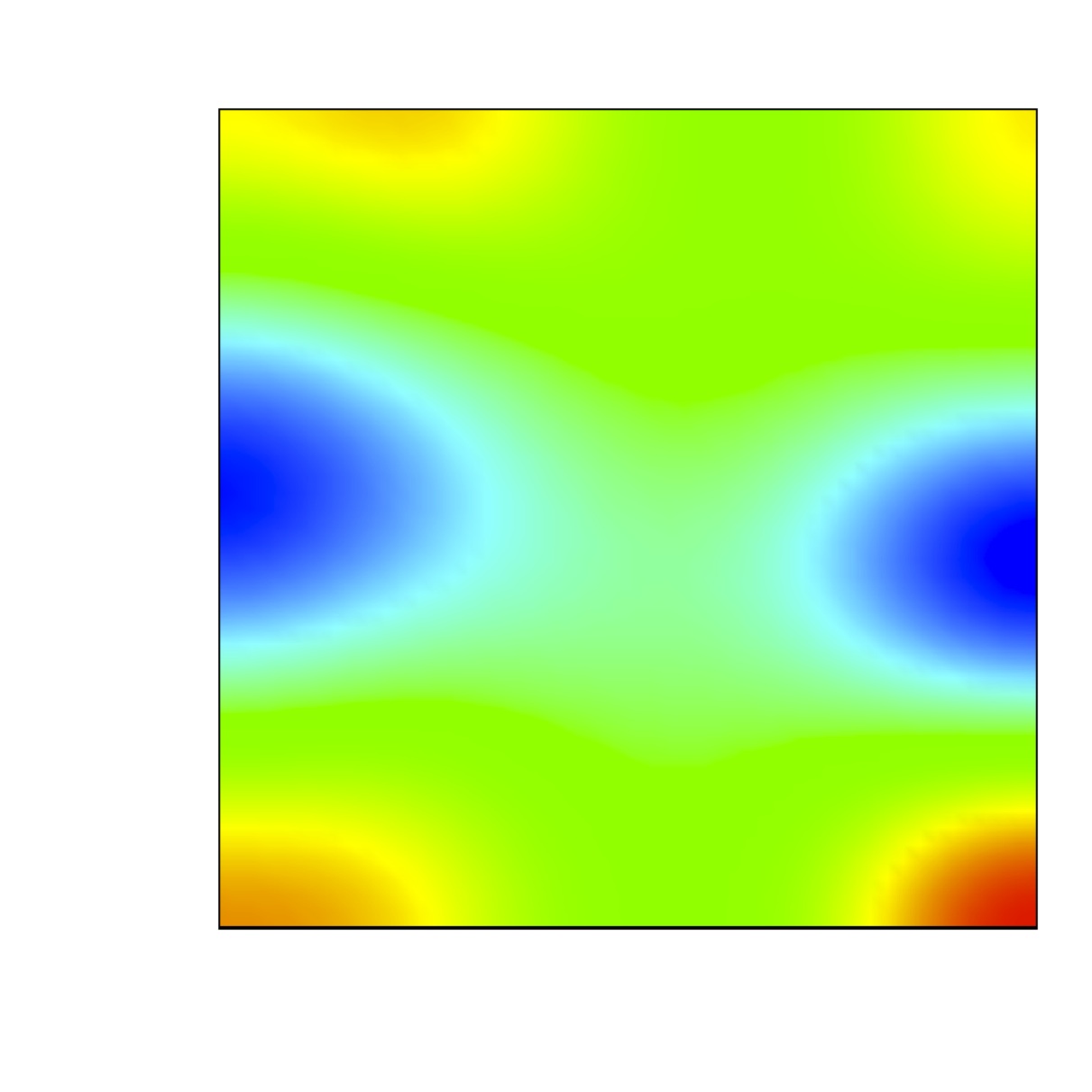
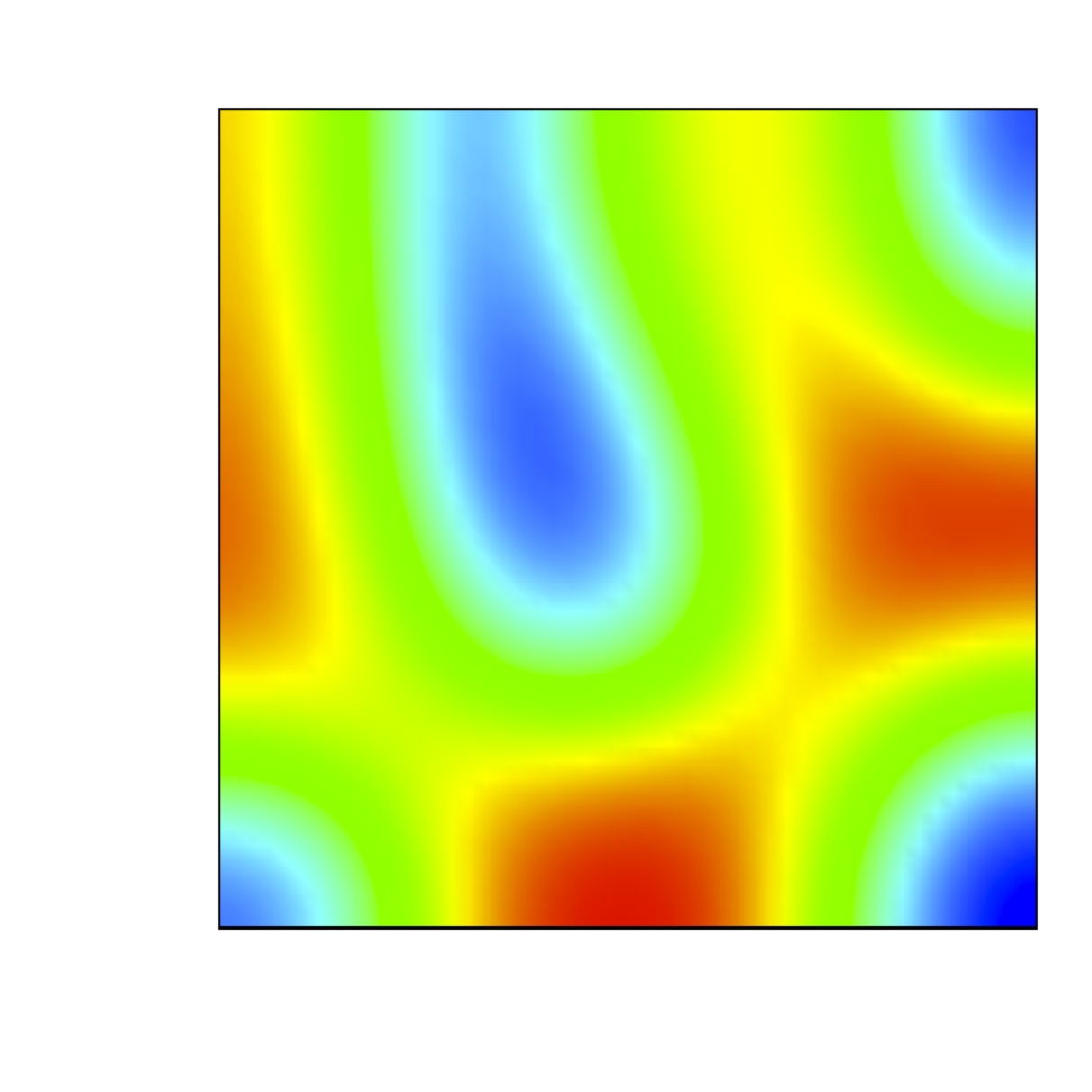
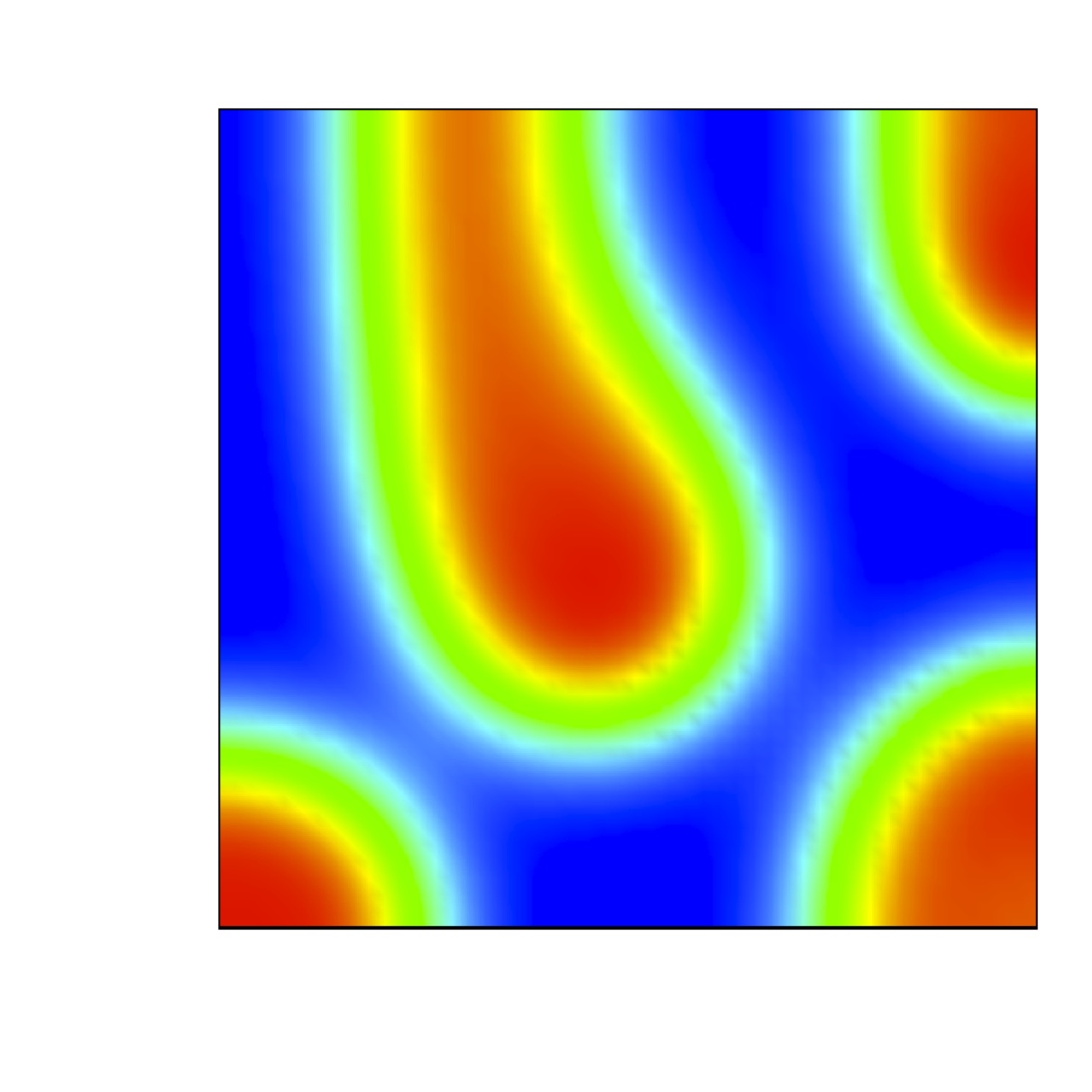
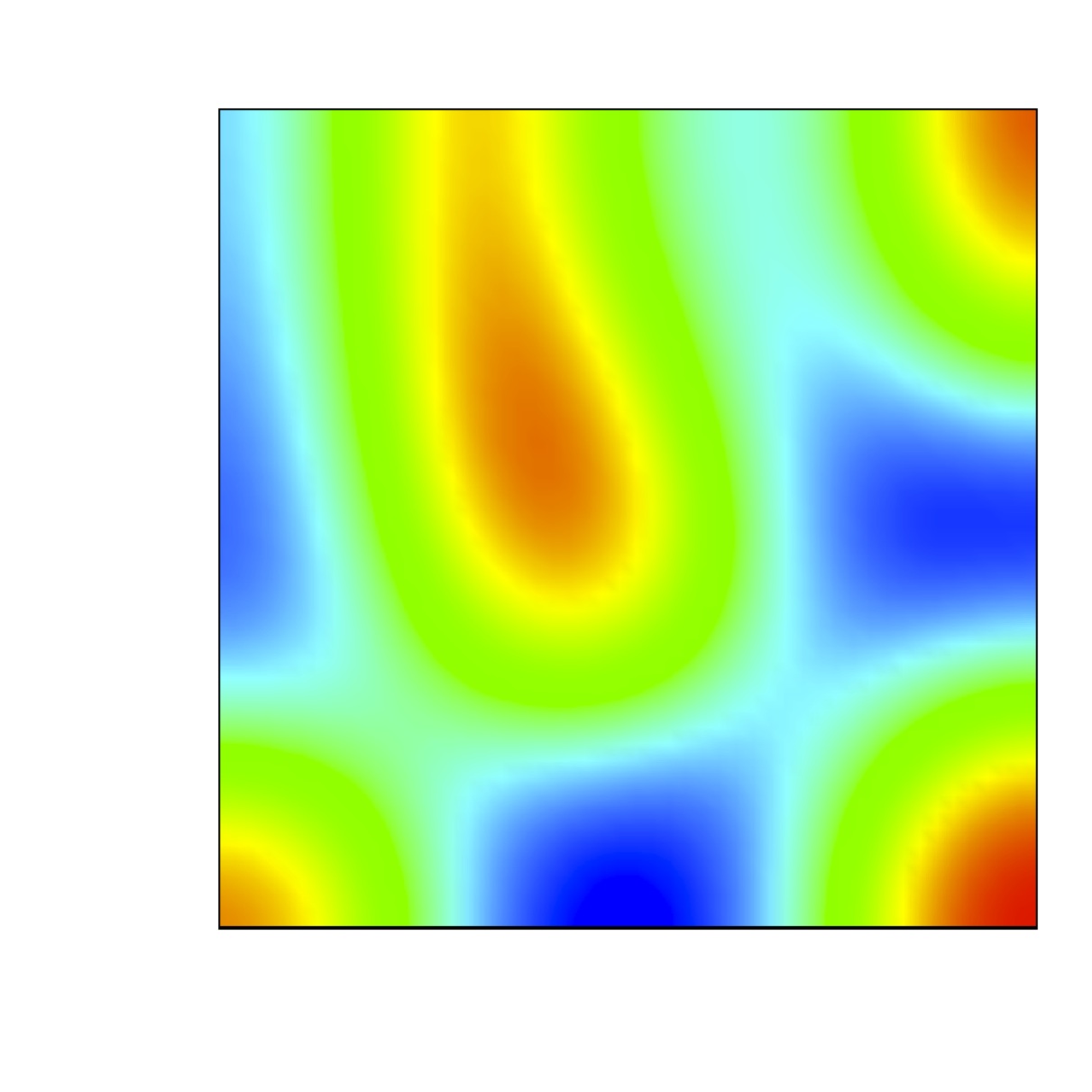
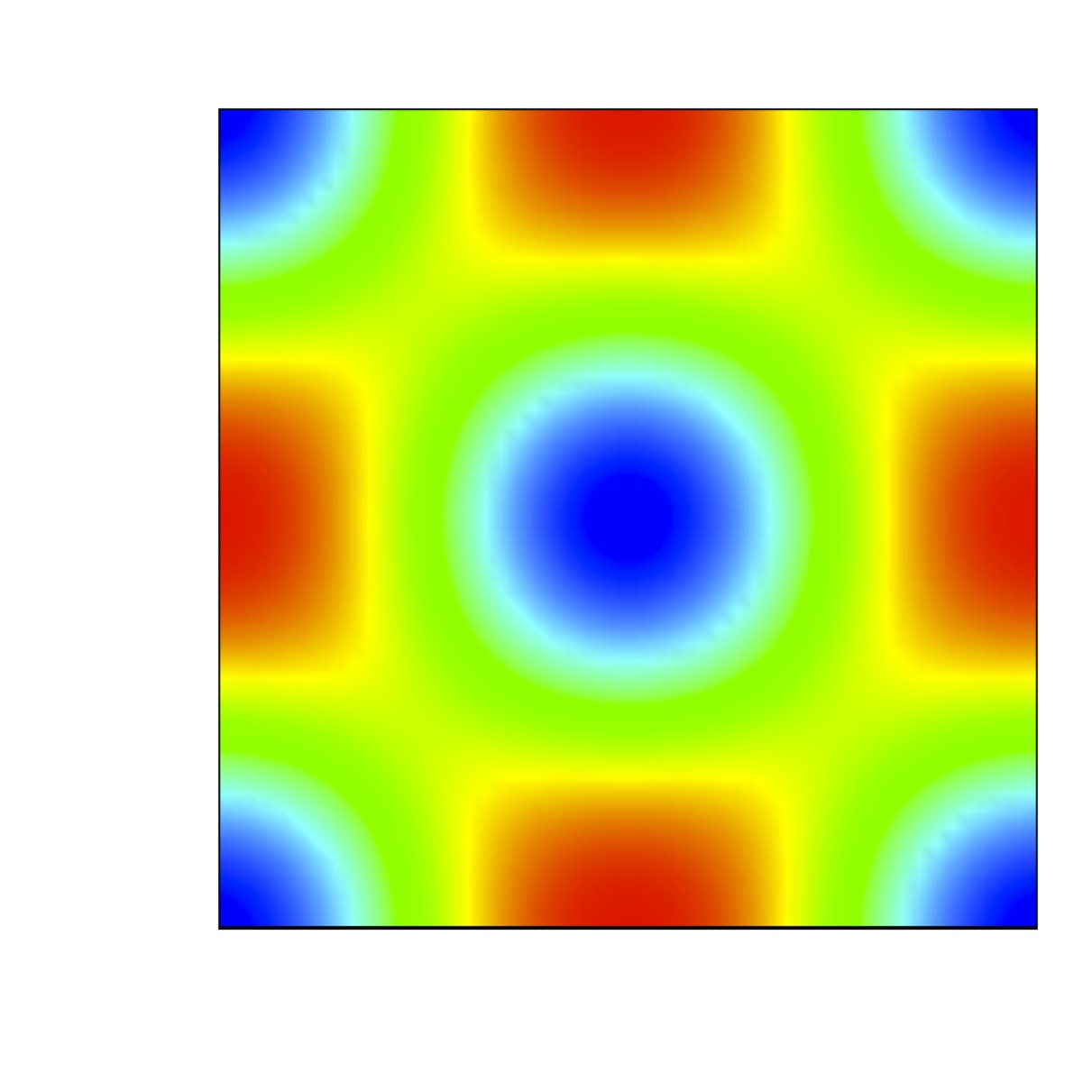
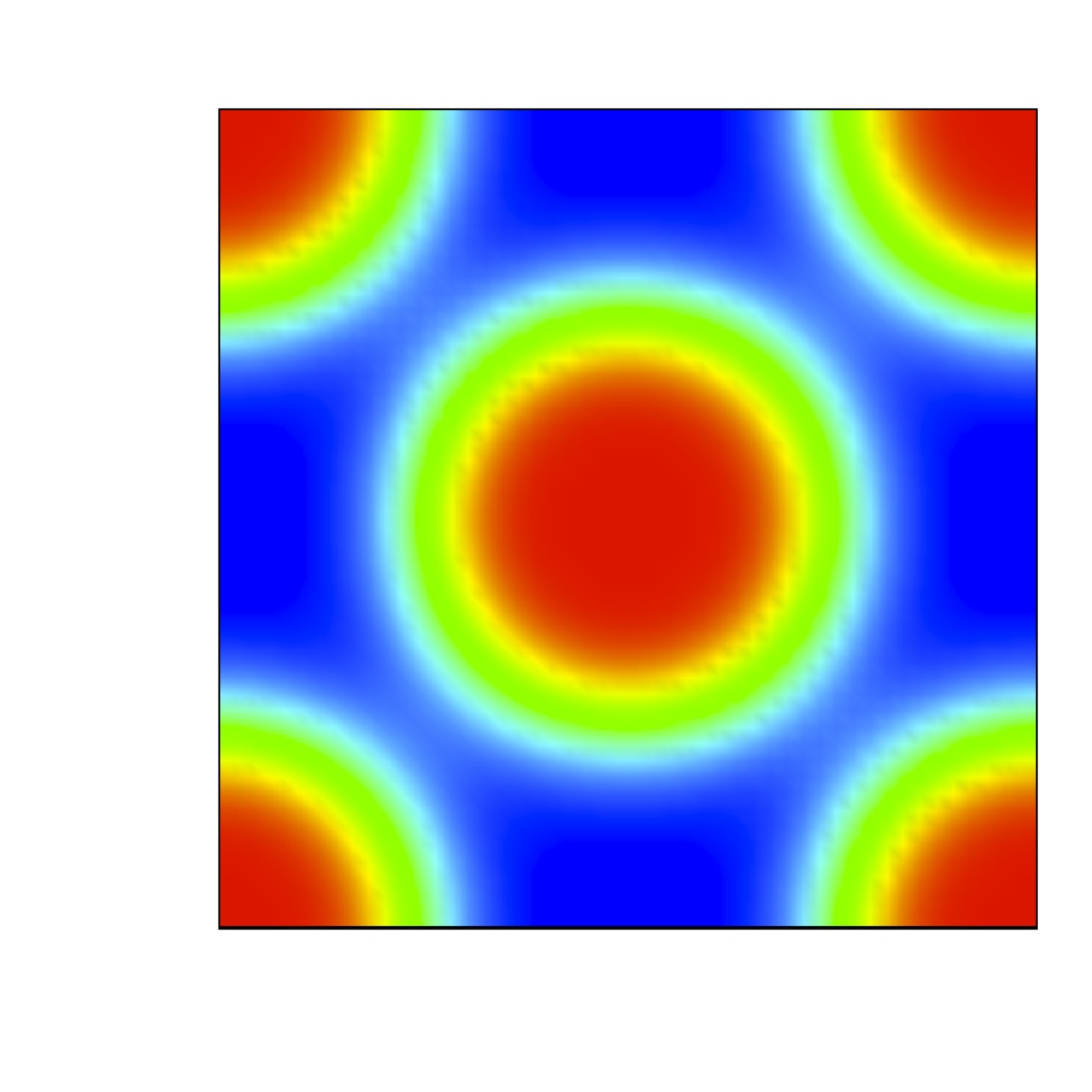
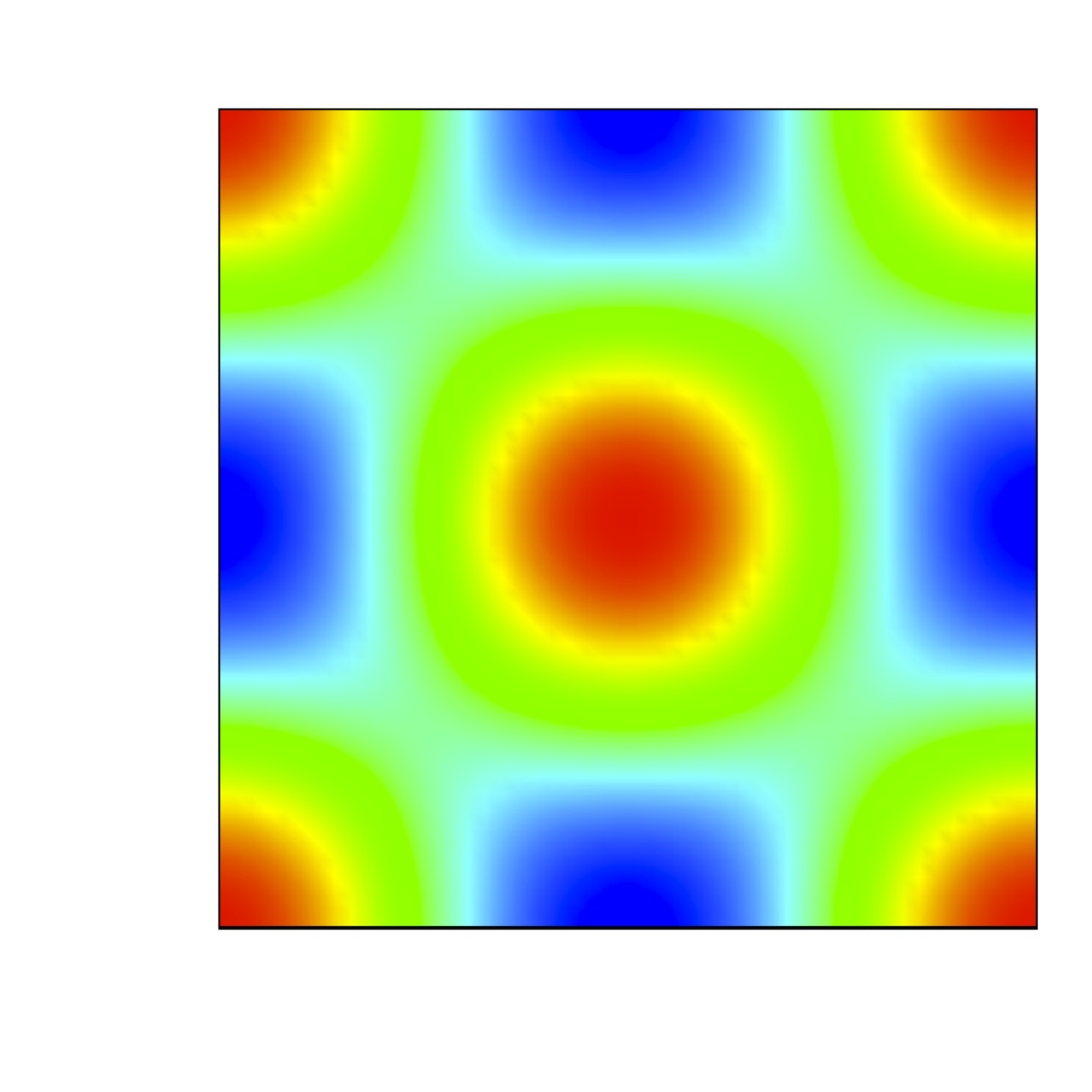
We are concerned with the formation of steady state
spatially heterogeneous spatial patterns for a simple model of
partial immunity model.
Turing conditions are exhibit for this model. Numerical results
show that a random perturbation around the steady uniform state in
the absence of diffusion can
generate a stationary nonuniform spatially state when the
diffusion are included.
Partial immunity and spatial diffusion:
The host population is divided into three proportions: susceptible
(u); infected (v); and recovered with reduced
susceptibility (w). The partial immunity model is build under the
assumption that individuals who have been previously infected and
recovered can be reinfected at a reduced rate.
Consider the initials conditions :
u(0,x,y)=u0(1+0.1 cos(3.14 n x) cos(3.14 m y))
v(0,x,y)= v0 (1+0.006 cos(3.14 n x) cos(3.14 m y) )
w(0,x,y)=1-u(0,x,y)-w(0,x,y)