Examen de Janvier 2001-LMA

Exercice 1. Que rend la fonction suivante :

  FUNCTION MYSTERE (STRING, TAILLE)
      IMPLICIT NONE
      INTEGER                  :: TAILLE
      CHARACTER (LEN = TAILLE) :: STRING
      CHARACTER                :: MYSTERE
      INTEGER                  :: J

      IF (TAILLE == 0) THEN 
         MYSTERE = ' '
      ELSE
         MYSTERE = STRING(1:1)
         DO J = 2, TAILLE
            IF ( STRING(J:J) < MYSTERE) MYSTERE = STRING(J:J)
         ENDDO
      ENDIF
   END FUNCTION MYSTERE

Effectuer les 'print' suivant :

PRINT*,' print 1 = ', MYSTERE('EXAMEN',6)
PRINT*,' print 2 = ', MYSTERE('YOYO',4)

Exercice 2. On désigne par T, Q, R des tableaux de rang un et U, V, W des tableaux de rang deux. Ecrire sous formes de boucles explicites les instructions suivantes :

Q(-1:9) = 2. * sin( T(1:11) )+ R
U(-2:9, 0:20 ) = U(-2:9, 0:20) + V( -1:10, 5:25) *  W(-1:10, 5:25)
U(4,:) = V(3,:)/Q + 5.
R = (/ (3.*i+1., i = 1, size(R)-2), -1., -2.  /)

Exercice 3.

Soit $A= (a_{ij})_{1\leq i,j \leq N}$ une matrice quelconque.

On décide de stocker uniquement les éléments non nuls de $A$, pour cela on considère la structure suivante :

        TYPE element
           REAL    :: coef
           INTEGER :: IndL, IndC
        END TYPE element

        TYPE(element), DIMENSION(:), ALLOCATABLE :: A

Dans la suite de l'exercice, toutes les matrices utilisées sont stockées sous cette forme.

1. Donnez la nature de ces objets :

            A,  A(i),  A(i)%coef,  A(i)%IndL, A(i)%IndC
          

2. On désigne par $A(I)\%coef$ le $ieme$ coefficient non nul de $A$ et par $A(I)\%IndL$ (respectivement $A(I)\%IndC$) l'indice de ligne (resp. l'indice de colonne) du coefficient $A(I)\%coef$. A titre d'exemple, la matrice suivante
   $$\left ( \begin{array}{cccc} -1. & 0 & 0 & 10.\\ 4. & 3. & 9. & 0 \\ 1. & 0 & 5. & 0 \\ 0 & -3. & 0 & 8. \end{array} \right )$$
   est stockée dans un fichier nommée $DATA.IN$ comme suit

    
   9              * nombre de coefficients non nuls de la matrice 
   -1.   1   1    * coef  indL  indC
    4.   2   1
    9.   2   3
   10.   1   4
    1.   3   1
   -3.   4   2
    3.   2   2
    8.   4   4
    5.   3   3
   

   Ecrire un procédure permettant de lire une matrice stockée sous cette forme.

3. Ecrire une fonction nommée FUNCTION TRACE(B) permettant de calculer la trace d'une matrice B. On rappelle que $trace(B) = \sum_{i = 1}^{N}b_{ii}$
4. Ecrire une fonction FUNCTION NORME(B) permettant de calculer la norme infinie d'une matrice B. On rappelle que $$\Vert B\Vert _\infty = \max_{j=1,N} (\sum_{i =1}^N \vert b_{ij}\vert )$$.

5. Ecrire une fonction : FUNCTION MfoixX(A, X) permettant de faire le produit d'une matrice $A$ par un vecteur $X$.

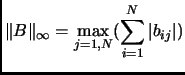   On pourra écrire dans un module une surdéfinition de l'opérateur ($\ast$), afinque l'opération suivante $C = A * X$ soit valide.

6. Soit la suite des vecteurs $(x_k)_k$ définie par :
   $$\left \{ \begin{array}{l} q_0 \mbox { donn\'ee tel que } \Ve... ...e 1\\ q_k = \frac{x_k}{\Vert x_k\Vert} \end{array} \right .$$
   où $\Vert \Vert$ désigne la norme euclidienne. Cette suite en module vers le rayon spectral, c-à-d la plus grande valeur propre en module, de la matrice $A$ ( on ne demande pas de faire la démonstration).

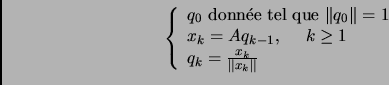
   Ecrire un programme permettant de calculer une approximation du rayon spectral d'une matrice A. On considère comme test d'arrêt pour cette méthode itérative : $\Vert x_k - x_{k-1}\Vert \leq \varepsilon.$ On peut eventuellement stocker le résultat dans un fichier de sortie.